ourvilla.blogg.se - Batch gradient descent

#Batch gradient descent update#
#Batch gradient descent code#

We’ll default this value to be 32 data points per mini-batch. We have already reviewed both the -epochs (number of epochs) and -alpha (learning rate) switch from the vanilla gradient descent example - but also notice we are introducing a third switch: -batch-size, which as the name indicates is the size of each of our mini-batches. Next, we can parse our command line arguments: # construct the argument parse and parse the argumentsĪp.add_argument("-e", "-epochs", type=float, default=100,Īp.add_argument("-a", "-alpha", type=float, default=0.01,Īp.add_argument("-b", "-batch-size", type=int, default=32, Lines 34 and 35 then loop over the training examples, yielding subsets of both X and y as mini-batches.

batchSize: The size of each mini-batch that will be returned.

y: The class labels associated with each of the training data points.

X: Our training dataset of feature vectors/raw image pixel intensities.

The next_batch method requires three parameters: # loop over our dataset "X" in mini-batches, yielding a tuple ofįor i in np.arange(0, X.shape, batchSize): However, what does change is the addition of the next_batch function: def next_batch(X, y, batchSize): # apply a step function to threshold the outputs to binary # take the dot product between our features and weight matrix In fact, the predict method doesn’t change either: def predict(X, W): Lines 9-17 define our sigmoid_activation and sigmoid_deriv functions, both of which are identical to the previous version of gradient descent. Lines 2-7 import our required Python packages, exactly the same as the gradient_descent.py example earlier in this chapter. # that the input "x" has already been passed through the sigmoid # compute the derivative of the sigmoid function ASSUMING # compute the sigmoid activation value for a given input Open a new file, name it sgd.py, and insert the following code: # import the necessary packagesįrom sklearn.model_selection import train_test_splitįrom trics import classification_report Let’s go ahead and implement SGD and see how it differs from standard vanilla gradient descent. For CPU training, you typically use one of the batch sizes listed above to ensure you reap the benefits of linear algebra optimization libraries. If you’re using a GPU to train your neural network, you determine how many training examples will fit into your GPU and then use the nearest power of two as the batch size such that the batch will fit on the GPU. In general, the mini-batch size is not a hyperparameter you should worry too much about ( ). Secondly, powers of two are often desirable for batch sizes as they allow internal linear algebra optimization libraries to be more efficient.

#Batch gradient descent update#

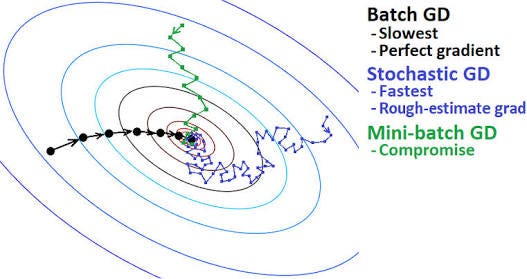
So, why bother using batch sizes > 1? To start, batch sizes > 1 help reduce variance in the parameter update ( ), leading to a more stable convergence. Typical batch sizes include 32, 64, 128, and 256. However, we often use mini-batches that are > 1.

In a “purist” implementation of SGD, your mini-batch size would be 1, implying that we would randomly sample one data point from the training set, compute the gradient, and update our parameters. From an implementation perspective, we also try to randomize our training samples before applying SGD since the algorithm is sensitive to batches.Īfter looking at the pseudocode for SGD, you’ll immediately notice an introduction of a new parameter: the batch size. We evaluate the gradient on the batch, and update our weight matrix W. Instead of computing our gradient over the entire data set, we instead sample our data, yielding a batch. The only difference between vanilla gradient descent and SGD is the addition of the next_training_batch function. Wgradient = evaluate_gradient(loss, batch, W) We can update the pseudocode to transform vanilla gradient descent to become SGD by adding an extra function call: while True: Instead, what we should do is batch our updates. It also turns out that computing predictions for every training point before taking a step along our weight matrix is computationally wasteful and does little to help our model coverage. For image datasets such as ImageNet where we have over 1.2 million training images, this computation can take a long time. The reason for this slowness is because each iteration of gradient descent requires us to compute a prediction for each training point in our training data before we are allowed to update our weight matrix. Reviewing the vanilla gradient descent algorithm, it should be (somewhat) obvious that the method will run very slowly on large datasets.

#Batch gradient descent code#

Looking for the source code to this post? Jump Right To The Downloads Section Mini-batch SGD